![[LinuxFocus Image]](../../common/January1998/border-short.jpg)
| Новости Архивы Компании Подсказки |
Программирование OpenGL: Рендеринг простых многоугольниковАвтор Miguel Angel Sepulveda |
Введение
Рисование точек
Рисование линий и многоугольников
Упражнения
В следующий раз...
ВведениеЭто первая статья в серии, посвященной OpenGL, который стал промышленным стандартом в 2D/3D графике (смотрите так же Что такое OpenGL?). Мы предполагаем, что читатель знаком со своей платформой для разработки программ на языке С, и немного знаком с библиотекой GLUT (в противном случае, ознакомьтесь с серией статей посвященных программированию GLUT в нашем журнале). Под Линуксом мы рекомендуем пользоваться библиотекой Mesa, которая является великолепной бесплатной реализацией стандарта OpenGL. В настоящее время есть даже аппаратная поддержка Mesa (смотрите графические карты 3Dfx). Каждая новая команда OpenGL будет сопровождаться примером, поясняющим ее работу; по крайней мере, мы постараемся придерживаться этого правила! К концу нашей серии статей мы представим Вашему вниманию исходный код игры-симулятора, полностью написанный на OpenGL. Прежде, чем я начну повествование, я хотел бы предупредить Вас, что я ученый, и почти весь мой опыт в общении с OpenGL заключался в создании моделей настоящих квантовых и классических систем. Поэтому мои примеры имеют легкий уклон ;-) Я надеюсь, читатели найдут эти примеры доступными для восприятия или, по крайней мере, забавными. Если Вы захотите взглянуть на другие примеры, просто дайте мне знать. OpenGL зачастую ассоциируется с трехмерной графикой, спецэффектами, сложными моделями с реалистичной имитацией освещения итд. Однако его можно использовать и как машину для двухмерного рендеринга. Это важно, так как Вы можете многому научиться на двухмерных моделях, прежде чем столкнетесь со всеми сложностями трехмерной перспективы, моделей, источников света, позиций камер итд. Большое количество инженерных и научных приложений могут быть созданы в двумерном пространстве. Итак, приступим для начала к изучению простой двухмерной анимации. Рисование точекOpenGL имеет всего лишь несколько геометрических примитивов: точки, линии и многоугольники. Все они описываются в терминах их соответствующих вершин. Вершина характеризуется двумя или тремя числами в формате с плавающей запятой, которые представляют собой Декартовы координаты этой вершины, (x,y) в двух- и (x, y, z) в трехмерном пространстве. Хотя Декартовы координаты являются наиболее общеупотребимыми, в компьютерной графике зачастую используется Гомогенная система координат, в которой каждая точка описывается четырьмя числами в формате с плавающей запятой, (x, y, z, w). Мы вернемся к системам координат после того, как опишем некоторые элементарные понятия трехмерного рендеринга. Поскольку все геометрические объекты в OpenGL в конечном счете описываются как упорядоченный набор вершин, есть целый набор функций для объявления вершин. Синтаксис функций таков: void glVertex{234}{sifd}[v](TYPE coords); Разберитесь хорошенько с приведенной записью. (Фигурные скобки представляют набор возможных и обязательных значений, например {234} означает 2 или 3 или 4, в то время как значение в квадратных скобках опционально и может быть опущено - Прим. Пер.) Фигурные скобки показывают часть имени функции. Функции могут иметь 2, 3 или 4 параметра в форматах: короткое целое, длинное целое, число с плавающей запятой или число с двойной точностью. Эти параметры опционально могут быть представлены в векторной форме, и в этом случае мы будем пользоваться функциями v-типа. Вот несколько примеров: void glVertex2s(1, 3);
float vector[3];
Для простоты все приведенные функции имеют общее имя glVertex*. Любая последовательность вершин интерпретируется OpenGL в соответствии с контекстом. Контекст объявляется парой функций glBegin(GLenum mode)
и glEnd(), любая функция glVertex* между приведенными выше функциями контекста интерпретируется в соответствии со значением режима - mode,
например:
нарисует нам 5 точек в двухмерном пространстве с указанными координатами. Константа GL_POINTS наряду с другими объявлена в заголовочном файле <GL/gl.h>. Есть много других режимов, но мы будем рассматривать их по мере необходимости Каждая точка рисуется цветом, хранящимся в переменной состоянии OpenGL, ассоциированной с буфером цветов. Чтобы изменить текущий цвет, используйте набор функций glColor*; о выборе цвета и манипуляции с ним можно говорить долго (этому будет посвящена отдельная статья). Пока же мы будем использовать три числа в формате с плавающей точкой в диапазоне от 0,0 до 1,0 в кодировке RGB (Red-Green-Blue, Красный-Зеленый-Синий);
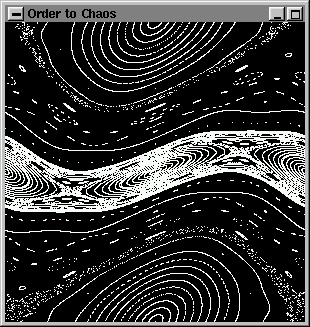
У нас уже достаточно материала, чтобы написать два первых примера. Первый - простая программа OpenGL для рисования множества орбит в так называемой хаотической карте (стандартной карте). Если читатель не знаком с картами, и в особенности со стандартной картой, не волнуйтесь. Проще говоря, карта берет точку и генерирует новую, используя широко известную формулу: yn+1 = yn + K sin(xn)
В случае стандартной карты мы получим модель траектории заряженной частицы, которая летает по кольцу ускорителя и пересекает его разделительную плоскость. Изучение свойств этой и других карт важно для физики, так как помогает понять стабильность зараженной частицы, заключенной в циклотрон. Стандартная карта весьма интересна, так как параметр К в точности показывает смесь хаотической и принудительной составляющих движения. В конце концов, даже те, кто совершенно не интересуются физикой, но все же хотят разрабатывать интересные программы для графики, должны обратить внимание на карты и их свойства, так как многие алгоритмы для создания текстур, языков пламени, деревьев, земной поверхности итд. основаны на фрактальных картах. Перед вами код первого примера ../../common/January1998/../../common/January1998/example1.c:
#include <GL/glut.h>
#include <math.h>
const double pi2 = 6.28318530718;
void NonlinearMap(double *x, double *y){
static double K = 1.04295;
*y += K * sin(*x);
*x += *y;
*x = fmod(*x, pi2);
if (*x < 0.0) *x += pi2;
};
void winInit(){
/* Установка системных координат */
gluOrtho2D(0.0, pi2, 0.0, pi2);
};
void display(void){
const int NumberSteps = 1000;
const int NumberOrbits = 100;
const double Delta_x = pi2/(NumberOrbits-1);
int step, orbit;
glColor3f(0.0, 0.0, 0.0);
glClear(GL_COLOR_BUFFER_BIT);
glColor3f(1.0, 1.0, 1.0);
for (orbit = 0; orbit < NumberOrbits; orbit++){
double x, y;
y = 3.1415;
x = Delta_x * orbit;
glBegin(GL_POINTS);
for (step = 0; step < NumberSteps; step++){
NonlinearMap(&x, &y);
glVertex2f(x, y);
};
glEnd();
};
for (orbit = 0; orbit < NumberOrbits; orbit++){
double x, y;
x = 3.1415;
y = Delta_x * orbit;
glBegin(GL_POINTS);
for (step = 0; step < NumberSteps; step++){
NonlinearMap(&x, &y);
glVertex2f(x, y);
};
glEnd();
};
};
int main(int argc, char **argv) {
glutInit(&argc, argv);
glutInitDisplayMode(GLUT_SINGLE | GLUT_RGBA);
glutInitWindowPosition(5,5);
glutInitWindowSize(300,300);
glutCreateWindow("Standard Map");
winInit();
glutDisplayFunc(display);
glutMainLoop();
return 0;
}
Прочтите статью Программирование
GLUT для понимания функций glut* , код в основном взят из той статьи. Графическое окно открывается в режиме одиночного буфера и RGB-палитры. Вызываемая функция с именем display() рисует карту: вначале мы выбираем черный цвет для фона; glClear(GL_COLOR_BUFFER_BIT) сбрасывает буфер цветов, устанавливая текущий цвет (черный), затем после выбора белого цвета с помощью glColor, запускает NonlinearMap() (Нелинейная Карта) множество раз и рисует точки функциями glVertex* в режиме GL_POINTS. Очень просто. :-)
Заметьте, что функция инициализации окна winInit()
содержит всего один вызов функции набора утилит OpenGL (GLUT), gluOrtho2D().
Эта функция устанавливает двухмерную прямоугольную систему координат. Параметрами функции являются "минимум x, максимум x, минимум y, максимум y".
По окончании работы примера вы увидите такое изображение:
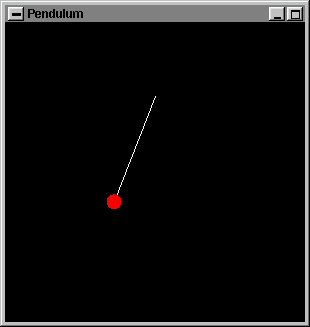
Давайте перейдем ко второй программе, ../../common/January1998/../../common/January1998/example2.c:
Другим заслуживающим внимания отличием является использование glutSwapBuffers()
в конце display(). Окно было проинициализировано в режиме двойного буфера, поэтому все операции по рисованию применяются к спрятанному буферу, и пользователь не видит, как прорисовывается изображение. По завершению отрисовки изображения (кадра), оно становится видимым переключением спрятанного и видимого буферов функцией glutSwapBuffers(). Без этой техники невозможно добиться плавной анимации.
Перед Вами некоторые из кадров, отображаемых во время анимации:
ВАЖНОЕ ЗАМЕЧАНИЕ: вызываемая функция display() всегда вызывается как минимум один раз перед функцией idle(). Принимайте этот факт во внимание при написании собственных анимационных программ, для того, чтобы решить, какие команды поместить в функцию display() а какие - в idle().
Как мы уже упоминали раньше, glBegin(GLenum mode) принимает в качестве параметра разные режимы (mode). Последовательность вершин v0, v1,v2,v3,v4,... vn-1 объявленных после этой функции интерпретируется соответственно выбранному режиму. Возможные значения для режимов и соответствующих действий:
Как и прежде, присутствует вызываемая функция idle() целью которой в данном случае является поддержание хода часов (изменением переменной time). Функция display() рисует два объекта: отвес (шнурок) и диск (белым и красным цветами соответственно). Движение маятника сокрыто в формулах для xcenter и ycenter:
Вот несколько предложений для практической работы над тем, что Вы только что изучили:
На сегодня все. Есть еще много недосказанного о многоугольниках.
В следующем выпуске (Март 1998) мы продолжим изучение многоугольников, моделирования и опишем более детально некоторые из команд, с которыми Вы уже успели познакомиться.
Перевод: Vladas Lapinskas
|
- Прочтите Обзор железа: Графические карты 3Dfx.
- Посетите http://www.opengl.org/.
- Прочтите другие статьи этого же автора: Что такое OpenGL?, Программирование GLUT: Окна и анимация.
This website is mantained by Miguel A Sepulveda.