DESA provides a comprehensive framework for early epidemic detection through school absenteeism surveillance. The package enables:
The methods implemented are based on research by Vanderkruk et al. (2023) and Ward et al. (2019).
Children typically have higher influenza infection rates than other age groups and are encouraged to stay home when ill. This makes school absenteeism data a valuable early indicator of community-wide epidemic arrival, potentially providing public health officials with crucial lead time to implement mitigation strategies.
Traditional epidemic surveillance systems often rely on laboratory-confirmed cases, which can introduce significant delays in detection. To address this limitation, Ward et al. (2019) investigated the use of school absenteeism data for early epidemic detection in the Wellington-Dufferin-Guelph region of Ontario, Canada.
The existing system in this region used a simple threshold-based approach (raising an alarm when 10% of students were absent) to identify potential outbreaks. Ward et al. developed detection models and introduced two evaluation metrics:
Building on this foundation, Vanderkruk et al. (2023) developed a more nuanced evaluation framework called Alert Time Quality (ATQ). Unlike the binary classification of previous metrics, ATQ assesses alerts where ones that are raised at sub optimal times receive penalties proportional to their deviation from the ideal alert time. This approach balances both accuracy and timeliness in a single metric.
The DESA package implements the methodologies from both papers, enabling users to:
You can install the development version of DESA from Github
#install.packages("devtools")
library(devtools)
install_github("vjoshy/DESA")The ATQ package includes the following main functions:
catchment_sim()
elementary_pop()
subpop_children()
subpop_noChildren()
simulate_households()
ssir()
compile_epi()
eval_metrics()
plot() and summary()
Additionally, the package implements S3 methods for generic functions:
plot() and summary()
ssir() and eval_metrics()plot() provides visualizations of epidemic simulations
and metric evaluationssummary() offers concise summaries of the simulation
results and metric assessmentsThese functions and methods work together to facilitate comprehensive epidemic simulation and evaluation of detection models
Please see example below:
# Load the DESA package
library(DESA)
set.seed(69420)
#Simulate number of elementary schools in each catchment
catch_df <- catchment_sim(16, 5, shape = 4.68, rate = 3.01)
# Simulate elementary school populations for each catchment area
elementary_df <- elementary_pop(catch_df, shape = 5.86, rate = 0.01)
# Simulate households with children
house_children <- subpop_children(elementary_df, n = 2,
prop_parent_couple = 0.7,
prop_children_couple = c(0.3, 0.5, 0.2),
prop_children_lone = c(0.4, 0.4, 0.2),
prop_elem_age = 0.6)
# Simulate households without children
house_nochildren <- subpop_noChildren(house_children, elementary_df,
prop_house_size = c(0.2, 0.3, 0.25, 0.15, 0.1),
prop_house_Children = 0.3)
# Combine household simulations and generate individual-level data
simulation <- simulate_households(house_children, house_nochildren)
# Extract individual-level data
individuals <- simulation$individual_sim
# Simulate epidemic using SSIR (Stochastic Susceptible-Infectious-Recovered) model
epidemic <- ssir(nrow(individuals), T = 300, alpha = 0.298, inf_init = 32, rep = 10)
# Summarize and plot the epidemic simulation results
summary(epidemic)
#> SSIR Epidemic Summary (Multiple Simulations):
#> Number of simulations: 10
#>
#> Average total infected: 41065.5
#> Average total reported cases: 826.9
#> Average peak infected: 3036.4
#>
#> Model parameters:
#> $N
#> [1] 136784
#>
#> $T
#> [1] 300
#>
#> $alpha
#> [1] 0.298
#>
#> $inf_period
#> [1] 4
#>
#> $inf_init
#> [1] 32
#>
#> $report
#> [1] 0.02
#>
#> $lag
#> [1] 7
#>
#> $rep
#> [1] 10
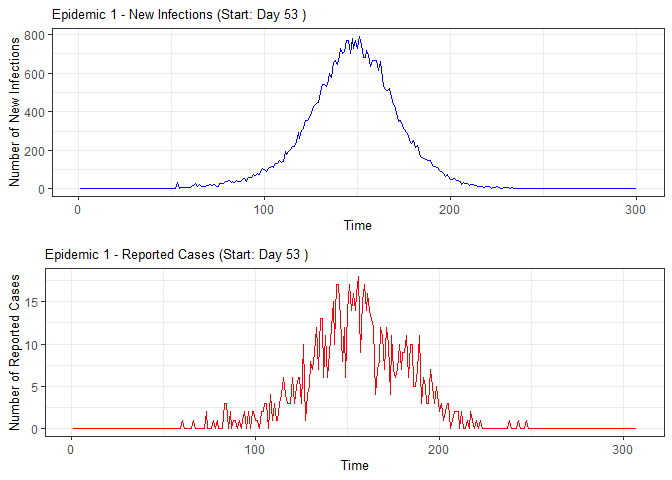
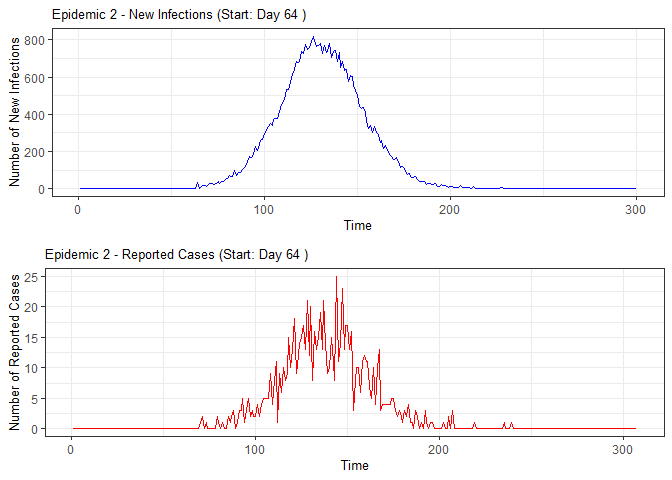
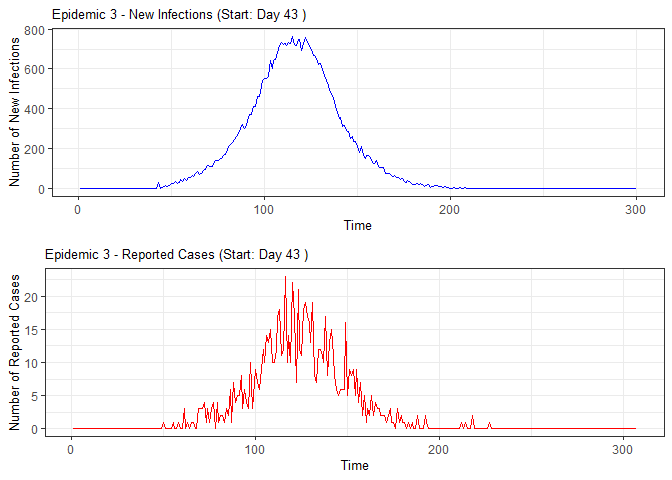
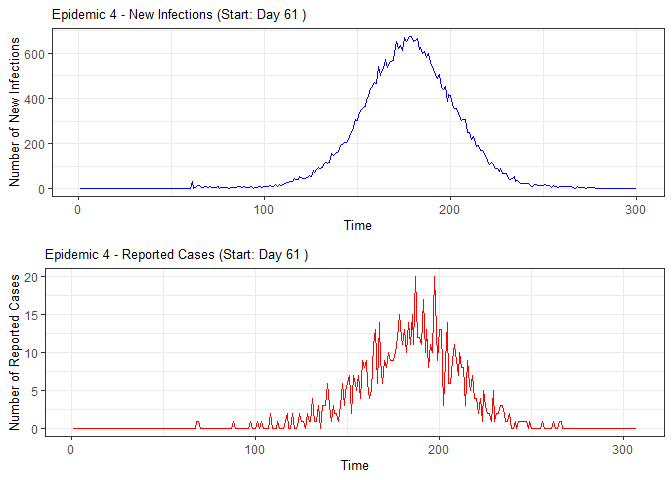
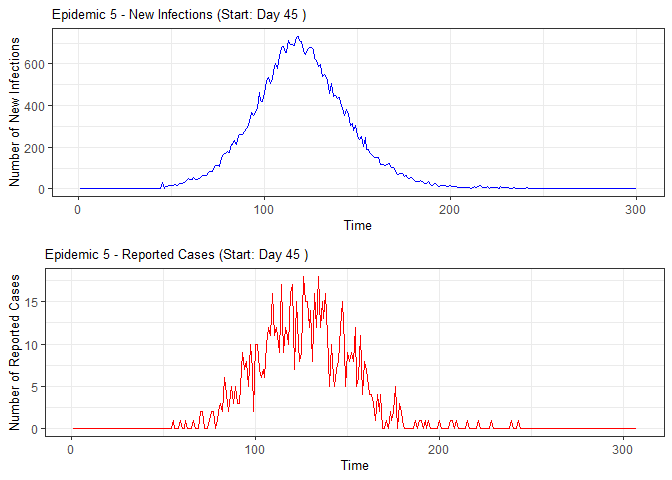
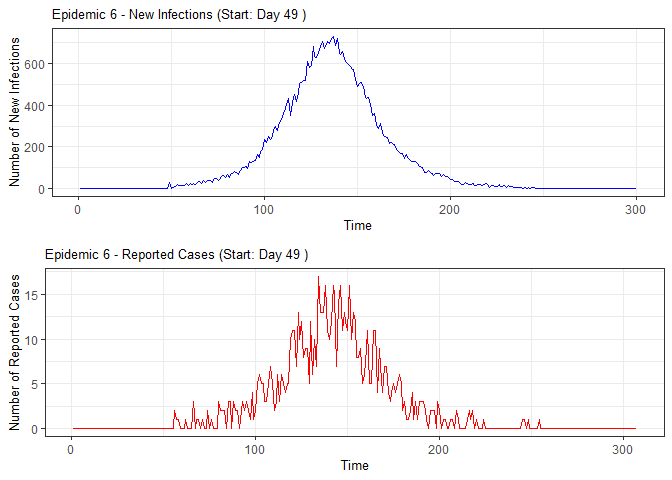
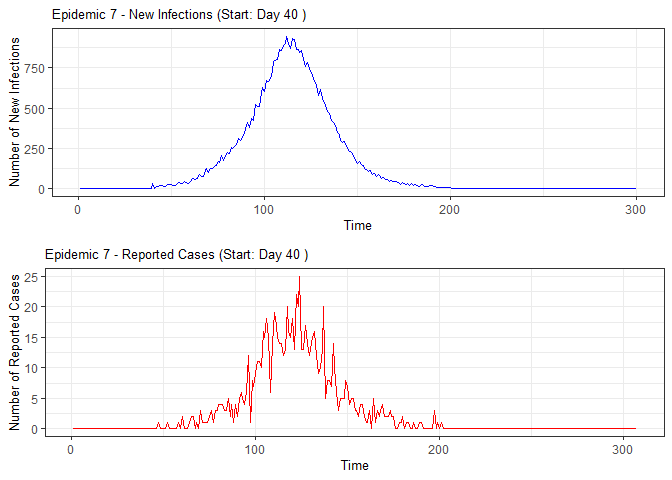
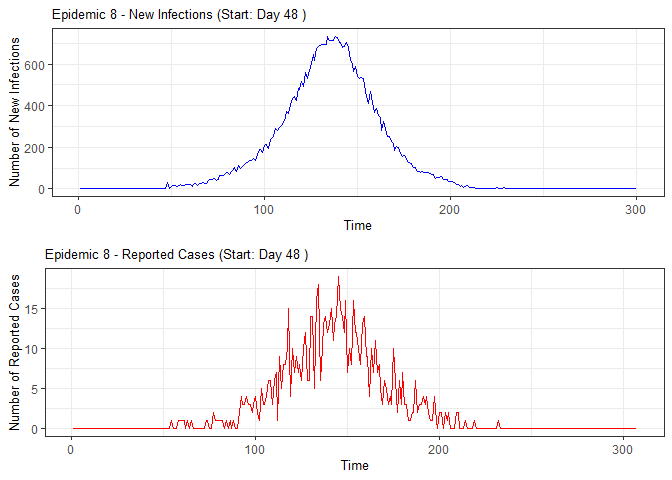
plot(epidemic)









# Compile absenteeism data based on epidemic simulation and individual data
absent_data <- compile_epi(epidemic, individuals)
# Display structure of absenteeism data
dplyr::glimpse(absent_data)
#> Rows: 3,000
#> Columns: 28
#> $ Date <int> 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17,…
#> $ ScYr <int> 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1…
#> $ pct_absent <dbl> 0.05096603, 0.05190044, 0.05079590, 0.04899765, 0.05083607…
#> $ absent <dbl> 636, 661, 628, 627, 623, 624, 607, 603, 657, 673, 616, 667…
#> $ absent_sick <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
#> $ new_inf <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
#> $ lab_conf <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
#> $ Case <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
#> $ sinterm <dbl> 0.01720158, 0.03439806, 0.05158437, 0.06875541, 0.08590610…
#> $ costerm <dbl> 0.9998520, 0.9994082, 0.9986686, 0.9976335, 0.9963032, 0.9…
#> $ window <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
#> $ ref_date <dbl> 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0…
#> $ lag0 <dbl> 0.05096603, 0.05190044, 0.05079590, 0.04899765, 0.05083607…
#> $ lag1 <dbl> NA, 0.05096603, 0.05190044, 0.05079590, 0.04899765, 0.0508…
#> $ lag2 <dbl> NA, NA, 0.05096603, 0.05190044, 0.05079590, 0.04899765, 0.…
#> $ lag3 <dbl> NA, NA, NA, 0.05096603, 0.05190044, 0.05079590, 0.04899765…
#> $ lag4 <dbl> NA, NA, NA, NA, 0.05096603, 0.05190044, 0.05079590, 0.0489…
#> $ lag5 <dbl> NA, NA, NA, NA, NA, 0.05096603, 0.05190044, 0.05079590, 0.…
#> $ lag6 <dbl> NA, NA, NA, NA, NA, NA, 0.05096603, 0.05190044, 0.05079590…
#> $ lag7 <dbl> NA, NA, NA, NA, NA, NA, NA, 0.05096603, 0.05190044, 0.0507…
#> $ lag8 <dbl> NA, NA, NA, NA, NA, NA, NA, NA, 0.05096603, 0.05190044, 0.…
#> $ lag9 <dbl> NA, NA, NA, NA, NA, NA, NA, NA, NA, 0.05096603, 0.05190044…
#> $ lag10 <dbl> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, 0.05096603, 0.0519…
#> $ lag11 <dbl> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, 0.05096603, 0.…
#> $ lag12 <dbl> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, 0.05096603…
#> $ lag13 <dbl> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, 0.0509…
#> $ lag14 <dbl> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, 0.…
#> $ lag15 <dbl> NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA, NA…
# Evaluate alarm metrics for epidemic detection
alarm_metrics <- eval_metrics(absent_data, thres = seq(0.1,0.6,by = 0.05))
# Plot various alarm metrics
plot(alarm_metrics$metrics, "FAR") # False Alert Rate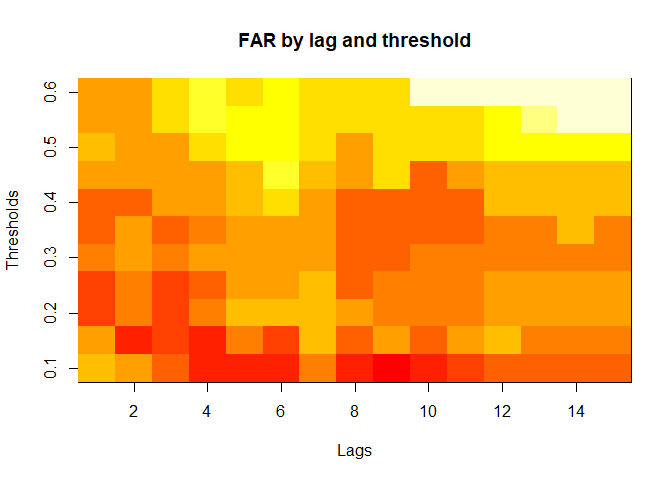
plot(alarm_metrics$metrics, "FATQ") # First Alert Time Quality
plot(alarm_metrics$metrics, "AATQ") # Average Alert Time Quality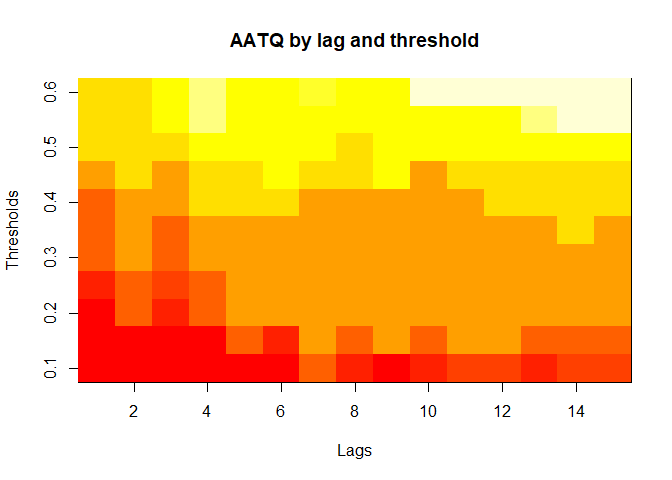
plot(alarm_metrics$metrics, "WAATQ") # Weighted Average Alert Time Quality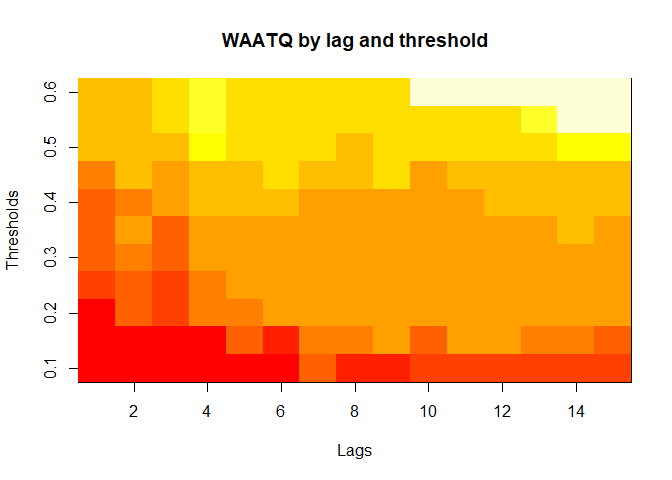
plot(alarm_metrics$metrics, "WFATQ") # Weighted First Alert Time Quality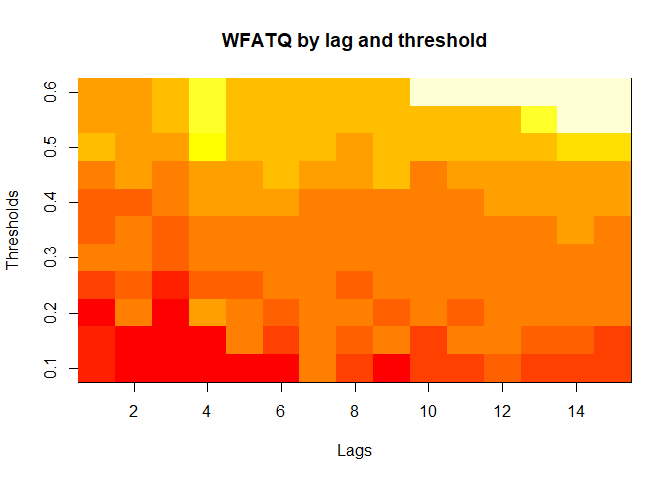
plot(alarm_metrics$metrics, "ADD") # Accumulated Delay Days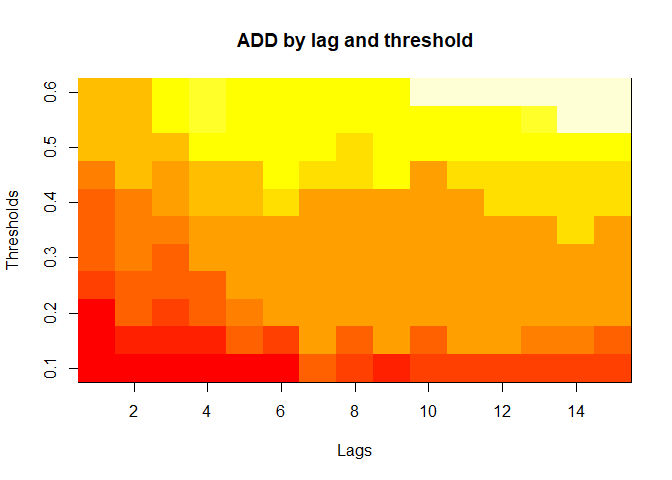
# Summarize alarm metrics
summary(alarm_metrics$results)
#> Alarm Metrics Summary
#> =====================
#>
#> FAR :
#> Mean: 0.5603
#> Variance: 0.0191
#> Optimal lag: 9
#> Optimal threshold: 0.1
#> Minimum value: 0.2111
#>
#> ADD :
#> Mean: 25.831
#> Variance: 75.0129
#> Optimal lag: 1
#> Optimal threshold: 0.1
#> Minimum value: 6.1111
#>
#> AATQ :
#> Mean: 0.542
#> Variance: 0.028
#> Optimal lag: 2
#> Optimal threshold: 0.1
#> Minimum value: 0.1861
#>
#> FATQ :
#> Mean: 0.5451
#> Variance: 0.0228
#> Optimal lag: 9
#> Optimal threshold: 0.1
#> Minimum value: 0.1964
#>
#> WAATQ :
#> Mean: 0.5288
#> Variance: 0.0313
#> Optimal lag: 1
#> Optimal threshold: 0.15
#> Minimum value: 0.1373
#>
#> WFATQ :
#> Mean: 0.5474
#> Variance: 0.0217
#> Optimal lag: 4
#> Optimal threshold: 0.1
#> Minimum value: 0.2516
#>
#> Reference Dates and Model Selected Alert Dates:
#> =====================
#>
#> year ref_date FAR ADD AATQ FATQ WAATQ WFATQ
#> 1 1 53 NA NA NA NA NA NA
#> 2 2 64 50 51 51 50 51 53
#> 3 3 43 42 NA NA 42 NA NA
#> 4 4 61 54 51 51 54 51 52
#> 5 5 45 45 33 34 45 33 33
#> 6 6 49 40 35 36 40 35 37
#> 7 7 40 31 31 30 31 37 31
#> 8 8 48 NA 35 41 NA 35 41
#> 9 9 61 55 47 50 55 50 55
#> 10 10 79 72 65 65 72 65 67
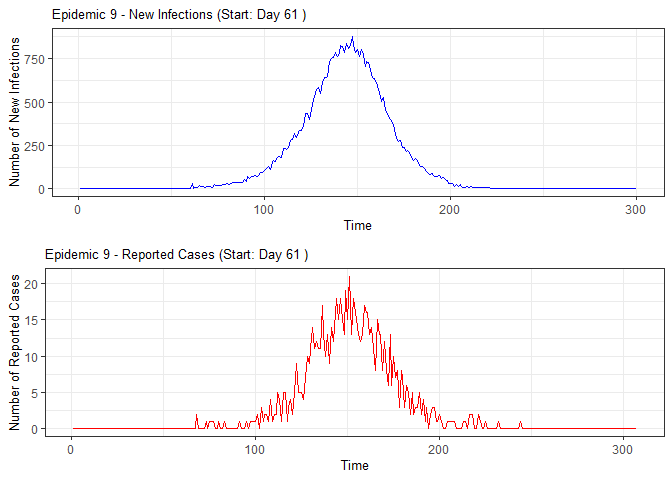
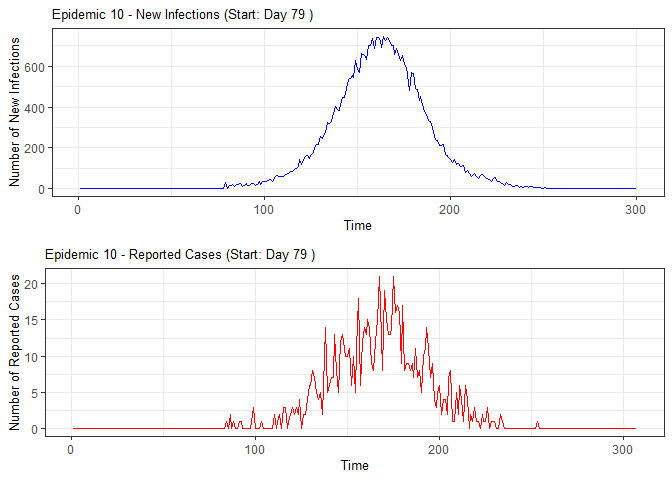
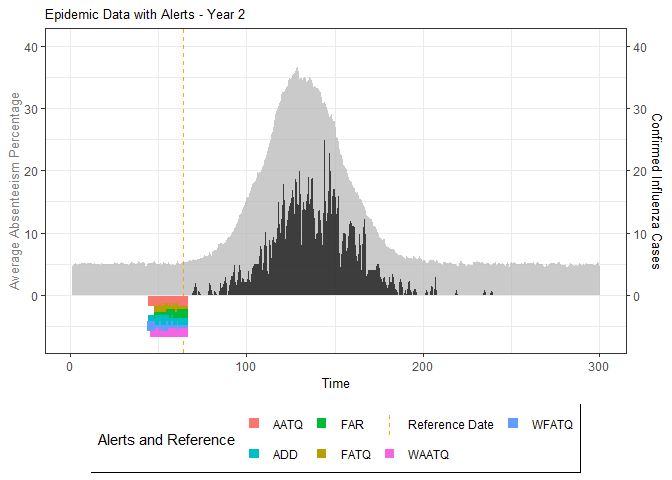
# Generate and display plots for alarm metrics across epidemic years
alarm_plots <- plot(alarm_metrics$plot_data)
for(i in seq_along(alarm_plots)) {
print(alarm_plots[[i]])
}
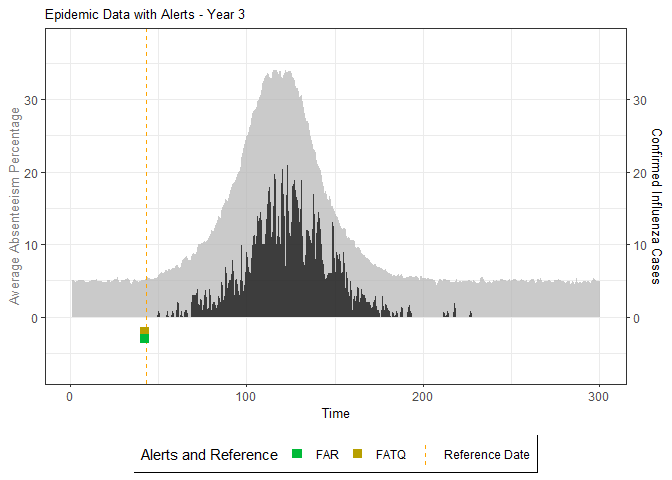
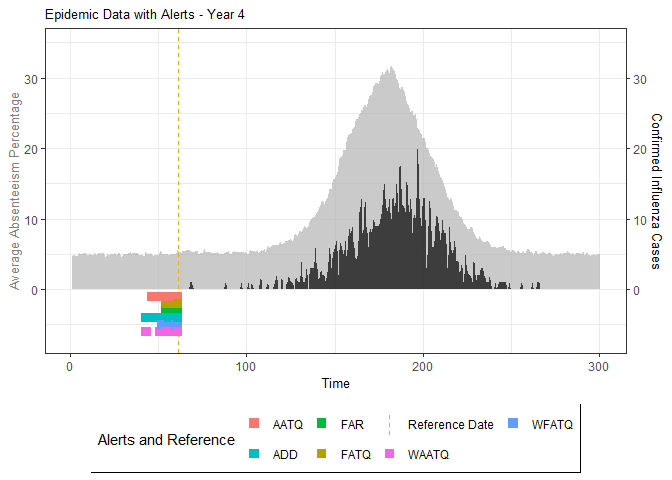
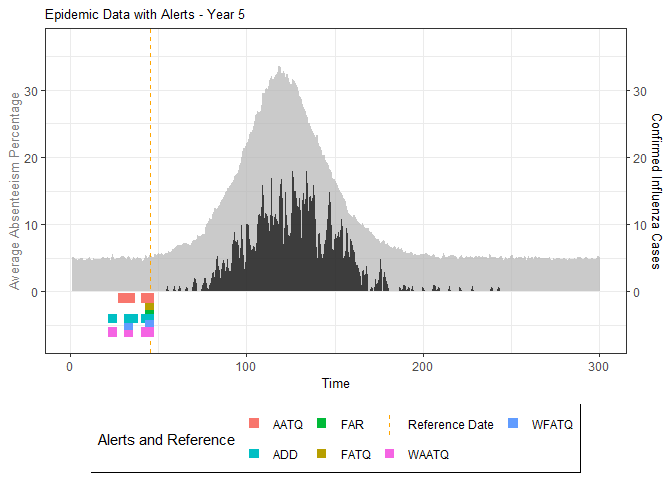
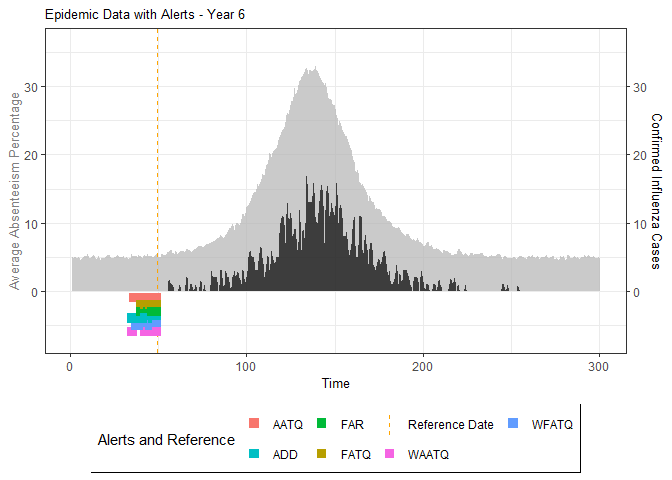
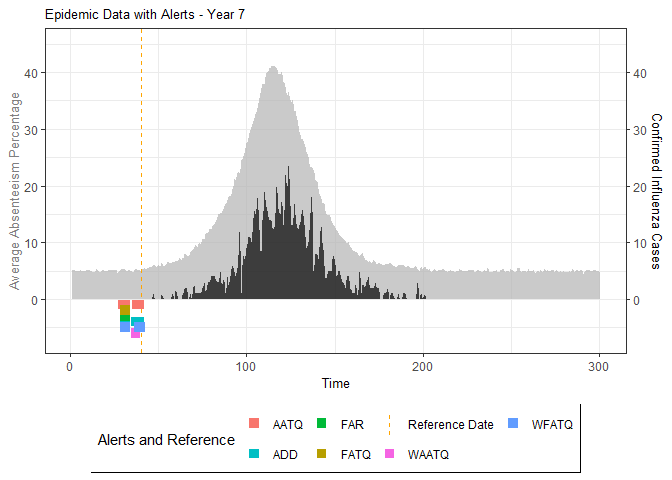
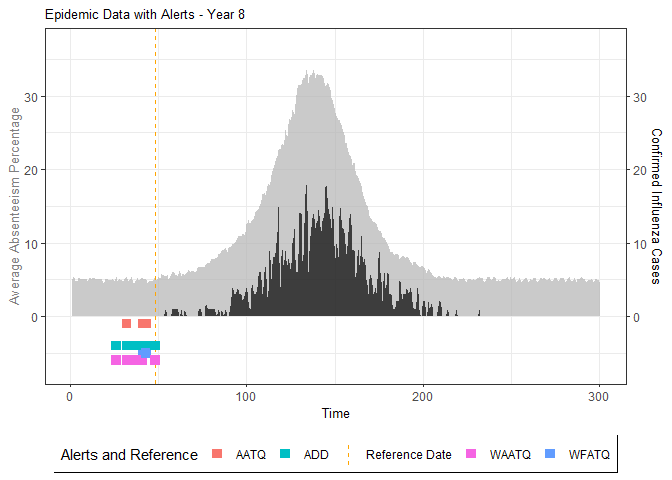
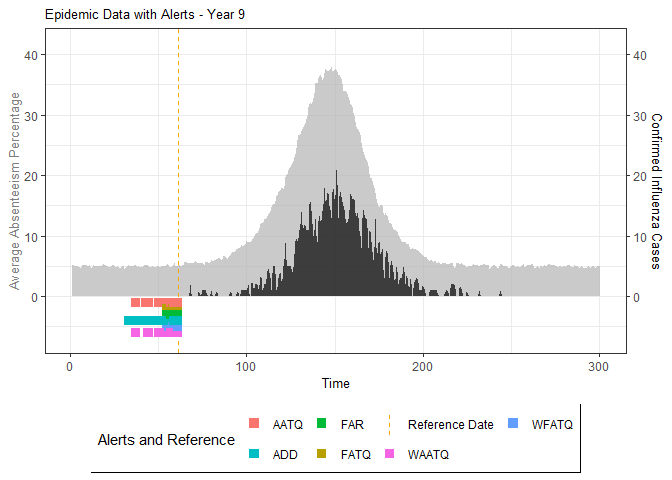
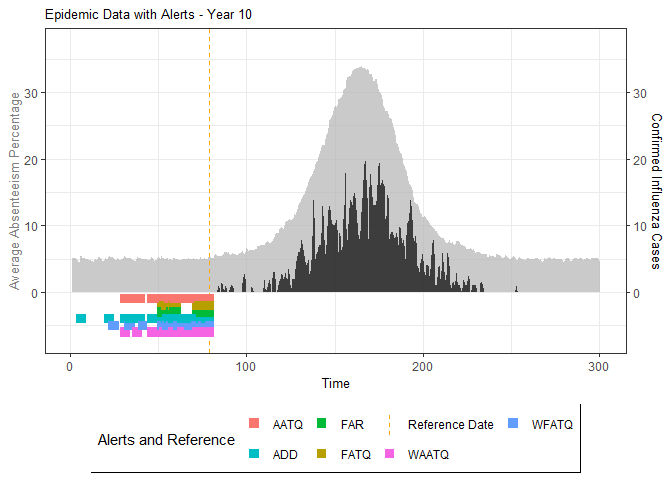
The final output region_metric will be a list of 6
matrices and 6 data frames. The matrices describe the values of metrics
for respective lag and thresholds.
An optimal lag and threshold value that minimizes each metric is selected and these optimal parameters are used to generate the 6 data frames associated with the metrics. Simulated information like number of lab confirmed cases, number of students absent, etc, are also included in the output.